Everything physical is information-theoretic in origin. This is the essence of the mantra “It from bit” coined by J. A. Wheeler to harp on the idea that quantum mechanics should be grounded in physical principles characterizing our reality rather than in a set of axioms that tells nothing about the world. And what is more fundamental and physical than information? Simply nothing: even the laws of physics do not apply to the objects that we probe in a laboratory, but only to the description of the world – to the information – that we obtain through experiment. In this view, quantum mechanics is the formal structure that describes how – and which – information about the world we can acquire and how our beliefs update as new information is gathered. So far, this paradigm-shifting attitude towards Nature has been resonating only within the gravity and quantum mechanics communities. The foundational quantum information theory group, led by Luca Marzola, aims to demonstrate the value of this approach by extending its scope to the field of particle physics.
The group researches the novel area located at the interface between particle physics and quantum information theory, ultimately aiming to produce a new description of the elementary phenomena of Nature built on the information-theoretic understanding of these processes. The work is done in collaboration with members of the Trieste INFN node, with the High energy physics and CMS data analysis groups located at KBFI, as well as with members of the the Institute of Computer Science of the University of Tartu within the initiatives of the Center of Excellence project TK202 “Foundations of the Universe”.
A first step towards our final goal is to apply quantum information theory methods to the fundamental processes probed in collider experiments. Key to the idea are the facts that:
Particles are inherently quantum objects that carry information, encoded for instance in their spin, flavor or symmetry representation. In fact, any property modeled with a compact Lie group naturally yields a quantum number that takes discrete values, allowing us to interpret particles as \( n \)-level systems and use the language of information theory. For instance, the possible spin states of an electron with respect to an arbitrary quantization direction allow us to think of this particle as of a two-level system carrying a bit of information. The two states – labelled \( \uparrow \) and \( \downarrow \), \( + \) and \( – \) or \( 0 \) and \( 1 \) – form the computational basis and span the Hilbert space used to describe the spin of an electron.Because quantum mechanics admits also states that are coherent superpositions of the basis states, an electron is more akin to a quantum bit – qubit, in short – than it is to a classical bit. As we can see, the superposition principle built in the linearity of the Schrödinger equation inexorably ushers us in the realm of quantum information theory. Here, particles are quantum information carriers.
The fundamental interactions described by the SM act as a source of entanglement. Let us consider a textbook example of process allowed by quantum electrodynamics: the annihilation of an electron-positron pair yielding the creation of a muon pair. Starting with unpolarized beams of electrons and positrons, we set off to investigate correlations between the spin vectors of the muons and anti-muons produced in repetitions of the process. Regarding these particles as qubits, we can resort to the density operator formalism and compute the 4×4 matrix that encodes the spin state of the muon-pair sample. Carrying out the computation, we then observe that the resulting density matrix cannot be written as a convex combination of Kronecker products involving the two density matrices that describe, separately, the polarization (i.e. the spin average) of the muon and anti-muon samples. In the language of quantum information theory, muons and anti-muons form a state that is not separable. This is in stark contrast with the density matrix of the electron-positron pairs that, by definition of initial state, must form a separable state. The notion of separability is central to quantum information theory and is strictly connected to another hallmark of quantum mechanics, entanglement: non-separable states are, by definition, entangled.
Returning to our example, it is then evident that the electromagnetic interaction responsible for the process has acted as a source of entanglement. This remarkable property, shared by all fundamental interactions, further motivates the use of QIT to investigate particle physics phenomena.
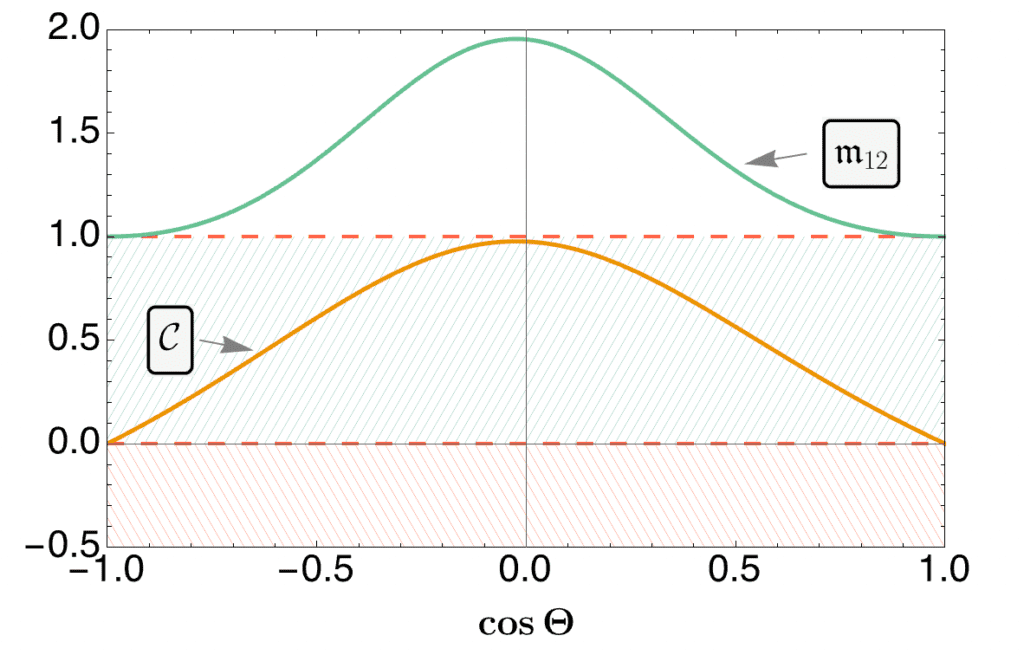
Following this line of research, the group already proved the feasibility of the approach by demonstrating that both the entanglement and the violation of the Bell inequality that this might entail can be probed at current and future collider experiments. As an example, the following plot shows the prospects for investigating these quantities by reconstructing the spin state of a pair of \( \tau \) leptons produced in a \( e^+ e^-\to Z\to \tau^+ \tau^- \) reaction at the \( Z \) boson resonance. Positive value of the concurrence, \( \mathscr{C} \), signal the presence of entanglement, while values of \( \frak{m}\)\(_{12}>1 \) imply the violation of the Bell inequality. The angle \( \Theta \) is the scattering angle between the direction of the \( \tau^+ \) lepton and the positron beam.
Besides investigating quantum mechanical phenomena such as entanglement and Bell inequality violation in the novel environment offered by high-energy physics experiments, the group is also capitalizing on the possibilities offered by quantum information theory within proper particle physics research. Quantum tomography, for instance, is a technique consisting in a series of measurements that yield the full reconstruction of the density matrix describing the system under investigation. Within particle physics, it can be used to test the Standard Model predictions against collider data with an accuracy as good as the experimental reconstruction can allow. In this context, the group has proved that the method can be used to strongly constrain the magnitude of anomalous couplings generated by potential new physics effects.
Quantum information theory is also well equipped to face the difficulties posed by the impossibility or impracticability of performing a complete tomographic measurement. In these cases, methods such as compressed sensing and classical shadows can be used to supplement the partial measurements available. The group aims also to explore the potential of these techniques applied to particle physics phenomenology, with special attention paid to final states containing invisible particles such as neutrinos, dark photons and most of the dark matter candidates proposed in the Literature. The research will also explore the idea that quantum cryptography and quantum error correction methods could play an important role in the study of backgrounds formed by elusive particles, such as the axion, that can effectively play the role of the eavesdropper or of quantum noise.
Finally, as we are developing the tools to describe particle physics phenomena in a quantum information theory language, it would be foolish not to explore the possible impact within high-energy physics of the more engineering side of the framework: quantum computing. This would yield at least two benefits: firstly, quantum computing is a field in rapid expansion and its potential applications to fundamental research are still vastly left untapped. In particular, a reliable protocol that could allow to perform simulations of high-energy phenomena at quantum computers is still missing. Secondly, quantum computers, per se, are laboratories where the quantum states used for the computation can be directly manipulated. It is then possible that quantum computers could be used to test the workings of quantum mechanics in yet another novel setting, contributing to bolster our understanding of the peculiar aspects of this theory. Part of the work of the group is then dedicated to the exploration of these novel research lines.